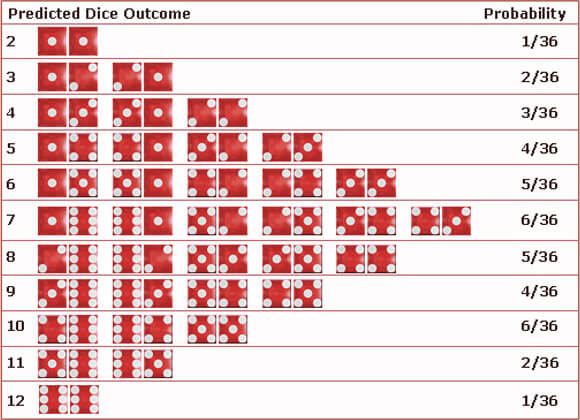
In the game of craps, two dice are rolled. If the sum is 2, 3, 7, 11, or 12, the game is over and the player either wins (in the case of 7 or 11) or loses (in the case of 2, 3, or 12). In any other case, the sum obtained becomes the player’s “point” and the game changes: Now, the player continues to roll two dice until the sum equals either 7 or the “point”. In the case of 7, the player loses; in the case of the “point”, the player wins; and in any other case, the player simply rolls again and nothing changes.
Find:
(a) P (player wins the “point” equals 4)
(b) P (player wins the “point” equals 5)
(c) P (player wins the “point” equals 6)
Finally, (d) show that the probability that a player wins a game of craps is exactly 244/495.
I'm sure I can figure out (b) and (c) after I figure out how to do part (a). I know that the chance of rolling a 4 would be 1/12, but I'm pretty sure there has to be more to the probability than that. I broke it up into:
P (player wins INTERSECT point equals 4) / P (point equals 4)
but I'm not sure what to do with the top.